From Galway with Bayes
Note: Traducción a espańol más abajo.
[ENG] Last week, SalGo team’s Connor Bernard and Jacque Deere headed to the west coast of Ireland to attend a BES Bayesian Macroecology workshop at NUI Galway. These are a few reflections from their trip by SalGo team PhD student Connor Bernard.

University Quadrangle at The National University of Ireland Galway.
The travel to Galway was about as good as one could hope for. I took an early flight to Galway in the interest of daylight*. This itinerary afforded me the privilege of sharing a shuttle to Heathrow with Prof Steven Stearns, who had been visiting Oxford and giving a seminar on senescence in days prior, making it one of the more enjoyable shuttle rides of my life. We talked life history, colorful corvids, and ageing – the good stuff. Once at Heathrow, the lines were nearly non-existent (for reasons that don’t warrant further comment here). Once on the plane, I had a seat row to myself and we were blessed with great views of the Pembrokeshire coast and Skomer Island.
* Meanwhile, Jacques was tending his flatworm commitments back on campus. He was not pleased to hear that I stole the better travel company.
The weather predictably failed to hold upon arrival. Jacques and I were met by cold rain followed by a brief torrent of snow. By the following day, we were back to patches of sunshine and rain. If there’s one thing we learned on this trip, it’s that priors can update quicker than you might hope – which applies to both weather and university operations.
The possibility of a closure of the university due to COVID-19 was mounting on Thursday morning, so we moved through the course content quickly. By noon, we were updated that there would only be a few more hours to learn everything there is to know about Bayesian statistics. The university was closing. It’s safe to say that Jacque and I learned a lot in that day – but mostly that Kevin Healy is a master of cram-teaching.
Day 1 – The focus of our Bayesian crash course was the practical mechanics of MCMCglmm models (Hadfield 2009;“Mac-Mac-Lamb” models) – their uses and potential misuses in the context of macro-ecology. Kevin Healy highlighted the advantages of a MCMCglmm-based modeling approach for regression-based analyses. He noted that you don’t need to be a prior-junkie or Bayesian evangelist to take advantage of the Bayesian approach and its flexibilities. Simply put, it’s okay to have uninformed priors and to be a glm-based Bayesian.
Along the way, we intersected some of the questions that have been on the SalGoers’ mind for the last few weeks: Notably, what do Bayesian approaches have to offer over Frequentist approaches? As discussed in last week’s SalGo #StatisticalRethinking group, there is a lot in common and a lot of overlap between the Frequentist and Bayesian camps [cue objections and yelling from both sides]. Many of us are yet to have conclusively resolved:
- Where do the relevant parts break down, exactly?
- When do the paths lead in seriously different directions and lead to materially different predictions and outcomes?
- Is it all just a matter of priors, or is there more subtlety?
We’ll get to that.
Step 1: The theorem. We started our morning the way that most modern scientists start their morning – with a healthy dose of caffeine and Bayes’ theorem. The Bayes’ theorem reflects a deceivingly straightforward statement – the reciprocal of the probability theorem that underlies frequentist statistics. Instead of asking whether data collected is consistent with a probability statement (hypothesis) – the frequentist perspective – Bayes asks whether a probability statement (hypothesis) is consistent with the data.
Frequentists: P(Evidence | Hypothesis)
What is the probability of evidence (i.e. data), given the hypothesis?
Bayesian: P(Hypothesis | Evidence)
What’s the probability of a hypothesis, given the data?
So how do we get at the P(H|E)? That’s where Bayes’ theorem comes in handy. For this brief note, I’m not going to walk through the underlying maths – you can find that in most stats books – but here’s the relevant expression:
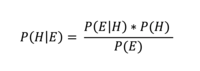
Where P(E|H) is the frequentist bit. Where P(H) is the prior. And where P(E) is the probability of observing the data (or all possible outcomes/the probability of everything). This P(E) element is a messy piece that we can ignore for now; but it is important because it normalizes the numerator.
Bayes in a nutshell: P(H|E) > P(E|H)
Step 2: MCMC and Me. The power of Multiple Chain Monti-Carlo (MCMC) methods is that they eliminate that messy part of Bayes’ theorem - the denominator (representing all possible outcomes). This, to my understanding, is formally called “the overly complex part of the equation that you shouldn’t worry about.”
The gist of these algorithms is that they simulate an iterative process that compares the parameter fit of one parameter to its neighboring parameter, and migrates according to some rule. If moving to a neighboring parameter is a better fit than the current parameter, then it moves, and repeats the process. With lots of independent iterations, the model converges on the best fitting parameters.
The model allows movement across parameter values according to specific rules/algorithms. As noted, this starts with the model looking at a neighboring parameter estimate and determining whether its current position is a better or worse fit (based on residual error with the observed data). If the neighboring estimate is better, it will move there, but – and this is key – only with a probability proportional to the difference in error (or some similar rule, depending on the specific algorithm). This probability piece affords room for the model to explore different parameter spaces, generating semi-random, error-minimizing exploration of a wide set of parameters.
The outcome of an MCMC simulation – which iterates thousands to millions of events – is a model that moves to and spends the most time/number of iterations within parameters of best fit. The model still spends time/iterations in parameters of less good fit proportional to the marginal improvement of the model fit, and in turn, with the probability that the parameter generated the data. Since the model uses neighbor-comparison as its rule for state-changing, it relies on a contrast ratio (fit 2/fit 1 > 1, then P(state 1 state 2)=(1/(fit 2:fit 1)). This rule allows the canceling of the denominator in Bayes’ Theorem.
I’ll spare the conversation about tinkering with specific models, burn-in, iteration counts, and so forth. The course was very helpful for walking through concrete examples of Bayesian tools to evaluate regression models.
Step 3: Priors. One of the biggest differences between the Bayesian approach and Frequentist approach is the existence of priors. The prior probability allows you to either clip out impossible values of a parameter distribution, or formally weight the distribution toward values as a function of knowledge about the system you are modeling. In either case, model fits improve as more constraints or prior knowledge is incorporated into the model (assuming it is accurate information).
Since priors can control the posterior distribution generated in Bayes’ approaches, you need to be thoughtful about the priors you choose. This seems to be one source of high contention between some Frequentists and Bayesians.
Back to that first question. Where do Frequentists and Bayesians break from one another? Kevin Healy raised a point that was novel to me about this question: In general, when you add more information into a Frequentist’s model without more data, you get into a situation where your likelihood estimates result in a division by zero, and the model computationally errs. By contrast, a Bayesian framework is prepared to accommodate lots of informational input and to estimate lots of parameters without running into impossible solutions. The long and short of this: You have flexibility to generate more complex models as well as incorporate more information into a simple model.
When you truly don’t have any informed priors (i.e. you’re using a flat, uniform prior), then the Frequentist and Bayesian approaches are materially one in the same most of the time. The main difference is different interpretations about the outputs (p-values versus posterior densities). But if you have priors - and many a Bayesian will tell you that you have more priors that you’re aware of - then the Bayesian approach will improve your model fit. If you’re running up against high-parameter estimation challenges, Bayes might also be your friend.
In the context of macroecology, Bayesian tools can be a liberating choice insofar as they free-up parameter estimation. Bayesian models are great at integrating lots of informational inputs as one might face in macro-ecological contexts. There is, of course, the converse consideration. We should not take Bayesian tools as license to complexify models for the sake of making them more complex; the biology should steer the level of complexity in our models.

The view from Rintinane Fort. A line of Oyster Catchers on the far left.
Days 2/3 - Jacque and I did our best MCMC impression, making our way around the city of Galway, randomly walking in search of better espresso. After a thorough but haphazard trip around the city, our top recommendation: Pascal’s - a quality cup in a neat little nook of downtown. After the obligatory stroll down the long walk, we made our way to the shoreside of Claddagh, Rintinane Fort, and Mutton Island. We found a vibrant bunch of Oyster Catchers (Haematopus ostralegus), stonechats (Saxicola rubicola), and a few feathered friends that we were about 70 percent sure were ringed plovers (Charadrius hiaticula). After an update from Jacque’s eBird maps, let’s call it 80 percent. Truth be told, I was equally captivated by the hooded crows (Corvus cornix) in downtown. I have a thing for corvids. Many a wool sweater shop later (and thoroughly impressed by the Aran Island knitwear), we ended our evenings with a swift half at the public house where we were warmly greeted by regional pub songs, along with a healthy dose of the Kilkenny’s and Oasis.
If you’re planning to learn Bayesian Statistics, we strongly recommend Galway.
[ESP] La semana pasada, los miembros del SalGo Connor Bernard y Jacques Deere se dirigieron a la costa oeste de Irlanda para asistir a un taller de macroecología bayesiana de BES en NUI Galway. Estas son algunas reflexiones de su viaje, escritas por Connor.
El viaje a Galway fue tan bueno como uno podría esperar. Tomé un vuelo temprano a Galway para aprovechar la luz del día*. Este itinerario me brindó el privilegio de compartir el autobus a Heathrow con el Profesor Steven Stearns, quien había estado visitando Oxford y dando un seminario sobre senescencia en días previos, lo cual lo convirtió en uno de los viajes en servicio más agradables de mi vida. Hablamos de la historias vitales, córvidos coloridos y la senescencia. Una vez en Heathrow, las líneas eran casi inexistentes (por razones que no justifican más comentarios aquí). Una vez en el avión, tuve una fila de asientos para mí solo y fuimos bendecidos con excelentes vistas de la costa de Pembrokeshire y la isla de Skomer.
* Mientras tanto, Jacques estaba atendiendo sus compromisos de planarias en el campus. No le agradó saber que robé la mejor compañía de viajes.
El clima no pudo mantenerse a la llegada, desafortunadamente. Jacques y yo nos encontramos con una lluvia fría seguida de un breve torrente de nieve. Al día siguiente, volvimos al intervitente cambio entre sol y lluvia. Si hay algo que aprendimos en este viaje, es que los previos pueden actualizarse más rápido de lo que cabría esperar, lo que se aplica tanto al clima como a las operaciones universitarias.
La posibilidad de un cierre de la universidad debido a COVID-19 aumentaba el jueves por la mañana, por lo que avanzamos rápidamente por el contenido del curso. Al mediodía, nos informaron que solo habría unas pocas horas más para aprender todo lo que hay que saber sobre las estadísticas bayesianas. La universidad estaba a punto de cerrarse. De seguro, Jacques y yo aprendimos mucho en ese día, pero sobre todo porque Kevin Healy es un maestro de la enseñanza express.
Día 1: El enfoque de nuestro curso intensivo bayesiano fue la mecánica práctica de los modelos MCMCglmm (Hadfield 2009; modelos "Mac-Mac-Lamb" [cordero en inglés]): sus usos y posibles abusos en el contexto de la macroecología. Kevin Healy destacó las ventajas de un enfoque de modelado basado en MCMCglmm para análisis basados en regresión. Señaló que no es necesario ser un adicto anterior o un evangelista bayesiano para aprovechar el enfoque bayesiano y sus flexibilidades. En pocas palabras, está bien tener antecedentes desinformados y ser un Bayesiano basado en glm.
De camino durante el currso, nos cruzamos con algunas de las preguntas que han estado en la mente de SalGoers durante las últimas semanas: Notablemente, ¿qué tienen para ofrecer los enfoques bayesianos sobre los enfoques frequentistas? Como se discutió en el grupo #StatisticalRethinking de SalGo de la semana pasada, hay mucho en común y mucha superposición entre los campamentos frequentista y bayesiano [objeciones de señal y gritos de ambos lados]. Muchos de nosotros aún no hemos resuelto de manera concluyente:
• ¿Dónde se descomponen exactamente las partes relevantes?
• ¿Cuándo los caminos conducen en direcciones muy diferentes y conducen a predicciones y resultados materialmente diferentes?
• ¿Es todo solo una cuestión de antecedentes, o hay más sutileza?
Paso 1: el teorema. Comenzamos nuestra mañana de la manera en que la mayoría de los científicos modernos comienzan su mañana, con una dosis saludable de cafeína y el teorema de Bayes. El teorema de Bayes refleja una afirmación engañosamente directa: el recíproco del teorema de probabilidad que subyace a las estadísticas frecuentistas. En lugar de preguntar si los datos recopilados son consistentes con una declaración de probabilidad (hipótesis), la perspectiva frecuentista, Bayes pregunta si una declaración de probabilidad (hipótesis) es consistente con los datos.
Frecuentistas: P (Evidencia | Hipótesis)
¿Cuál es la probabilidad de evidencia (es decir, datos), dada la hipótesis?
Bayesiano: P (Hipótesis | Evidencia)
¿Cuál es la probabilidad de una hipótesis, dados los datos?
Entonces, ¿cómo llegamos a la P (H | E)? Ahí es donde el teorema de Bayes es útil. Para esta breve nota, no voy a repasar las matemáticas subyacentes, puedes encontrar eso en la mayoría de los libros de estadísticas, pero aquí está la expresión relevante:
Donde P (E | H) es el bit frecuentista. Donde P (H) es el anterior. Y donde P (E) es la probabilidad de observar los datos (o todos los resultados posibles / la probabilidad de todo). Este elemento P (E) es una pieza desordenada que podemos ignorar por ahora; pero es importante porque normaliza el numerador.
Bayes, en pocas (o ningunas!) palabras: P (H | E)> P (E | H)
Paso 2: MCMC y yo. El poder de los métodos de Cadena Múltiple Monti-Carlo (MCMC) es que eliminan esa parte desordenada del teorema de Bayes: el denominador (que representa todos los resultados posibles). A mi entender, esto se llama formalmente "la parte demasiado compleja de la ecuación por la que no debe uno preocuparse demasiado".
La esencia de estos algoritmos es que simulan un proceso iterativo que compara el ajuste del parámetro de un parámetro con su parámetro vecino y migra de acuerdo con alguna regla. Si moverse a un parámetro vecino se ajusta mejor que el parámetro actual, entonces se mueve y repite el proceso. Con muchas iteraciones independientes, el modelo converge en los mejores parámetros de ajuste.
El modelo permite el movimiento a través de valores de parámetros de acuerdo con reglas / algoritmos específicos. Como se señaló, esto comienza con el modelo mirando una estimación de parámetros adyacentes y determinando si su posición actual es mejor o peor (en base a un error residual con los datos observados). Si la estimación vecina es mejor, se moverá allí, pero, y esta es la clave, solo con una probabilidad proporcional a la diferencia de error (o alguna regla similar, dependiendo del algoritmo específico). Esta pieza de probabilidad ofrece espacio para que el modelo explore diferentes espacios de parámetros, generando una exploración semialeatoria que minimiza los errores de un amplio conjunto de parámetros.
El resultado de una simulación MCMC, que itera de miles a millones de eventos, es un modelo que se mueve y pasa la mayor cantidad de tiempo / número de iteraciones dentro de los parámetros de mejor ajuste. El modelo aún pasa tiempo / iteraciones en parámetros de menor ajuste proporcional a la mejora marginal del ajuste del modelo y, a su vez, con la probabilidad de que el parámetro genere los datos. Dado que el modelo utiliza la comparación de vecinos como regla para cambiar el estado, se basa en una relación de contraste (ajuste 2 / ajuste 1> 1, luego P (estado 1 estado 2) = (1 / (ajuste 2: ajuste 1)) Esta regla permite cancelar el denominador en el Teorema de Bayes.
Me ahorraré la conversación sobre retoques con modelos específicos, quemados, recuentos de iteraciones, etc. El curso fue muy útil para recorrer ejemplos concretos de herramientas bayesianas para evaluar modelos de regresión.
Paso 3: Priors. Una de las mayores diferencias entre el enfoque bayesiano y el enfoque frequentista es la existencia de prios. La probabilidad previa (prios) le permite a uno descartar valores imposibles de una distribución de parámetros o ponderar formalmente la distribución hacia valores en función del conocimiento sobre el sistema que está modelando. En cualquier caso, los ajustes del modelo mejoran a medida que se incorporan más restricciones o conocimientos previos al modelo (suponiendo que sea información precisa).
Dado que los priors pueden controlar la distribución posterior generada en los enfoques de Bayes, debe tenerse en cuenta los priors que se elijan. Esto parece ser una fuente de gran controversia entre algunos frequentistas y bayesianos.
De vuelta a esa primera pregunta. ¿Dónde están en desacuerdo los frequentistas y los bayesianos? Kevin Healy planteó un aspecto que era nuevo para mí sobre esta pregunta: en general, cuando agrega uno más información al modelo de un frequentista sin más datos, se encuentra uno en una situación en la que sus estimaciones de probabilidad dan como resultado una división por cero, y el modelo computacionalmente erra. Por el contrario, un marco bayesiano está preparado para acomodar una gran cantidad de información y estimar muchos parámetros sin encontrar soluciones imposibles. En resumen: tiene flexibilidad para generar modelos más complejos, así como para incorporar más información en un modelo simple.
Cuando realmente no se tienen priors informados (es decir, está utilizando un prior plano y uniforme), los enfoques Frequentista y Bayesiano son materialmente iguales la mayor parte del tiempo. La principal diferencia son las diferentes interpretaciones sobre los resultados (valores p versus densidades posteriores). Pero si tiene antecedentes, y muchos bayesianos dirán que tiene más priors de los que se conoce algo, entonces el enfoque bayesiano mejorará el ajuste del modelo. Si te enfrentas a desafíos de estimación de muchos parámetros, Bayes también podría ser tu amigo.
En el contexto de la macroecología, las herramientas bayesianas pueden ser una opción liberadora en la medida en que liberan la estimación de parámetros. Los modelos bayesianos son excelentes para integrar muchos aportes informativos tipicos de contextos macroecológicos. Existe, por supuesto, la consideración inversa. No deberíamos tomar las herramientas bayesianas como licencia para construir modelos con el fin de hacerlos más complejos de lo necesario; La biología debe dirigir el nivel de complejidad en nuestros modelos.
Días 2/3: Jacques y yo hicimos nuestra mejor impresión de MCMC, recorriendo la ciudad de Galway, caminando al azar en busca de un mejor café expreso. Después de un viaje minucioso pero fortuito por la ciudad, nuestra principal recomendación: Pascal's, una taza de calidad en un pequeño rincón del centro. Después del paseo obligatorio por la larga caminata, nos dirigimos a la orilla de Claddagh, Rintinane Fort y Mutton Island. Encontramos un grupo vibrante de ostreros (Haematopus ostralegus), culiblancos (Saxicola rubicola) y algunos amigos emplumados de los que estábamos seguros en un 70 por ciento de chorlitos (Charadrius hiaticula). Después de una actualización de los mapas eBird de Jacques, llamémosla 80 por ciento. A decir verdad, estaba igualmente cautivado por los cuervos encapuchados (Corvus cornix) en el centro. Tengo una preferencia por los córvidos. Más tarde, en una tienda de suéteres de lana (y completamente impresionados por los géneros de punto de la isla de Aran), terminamos nuestras noches con una media pinta en un pub donde nos recibieron calurosamente las canciones regionales, junto con una buena dosis de Kilkenny's y Oasis.
Si planea aprender Estadísticas Bayesianas, te recomendamos encarecidamente Galway.
Traducido a español por Rob S-G // Translated to Spanish by Rob S-G



